еЗЇеЉµеЕИгБІиЕєгБМжЄЫгБ£гБЯжЩВгАБгБµгБ®еЙНгВТи¶ЛгВЛгБ®гБЭгБУгБЂгГ©гГЉгГ°гГ≥е±ЛгАВ
гГБгВІгГЉгГ≥еЇЧгБІгБѓгБ™гБПгАБи¶ЛгБЯгБУгБ®гВВгБ™гБДеЇЧеРНгБІгБЩгАВ
гБУгБЖгБДгБЖгБЃгБ£гБ¶гАБеЕ•гВЛгБЃгБЂгБ°гВЗгБ£гБ®еЛЗж∞ЧгБДгВКгБЊгБЩгВИгБ≠пЉЯ
гБІгВВдїКгБѓгБ®гБ¶гВВиЕєгБМжЄЫгБ£гБ¶гБДгВЛгАВ
гБїгБЛгБЂеЇЧгВВи¶ЛељУгБЯгВЙгБ™гБДгБЧгАБиГМгБЂиЕєгБѓгБЛгБИгВЙгВМгВУгАВ
жАЭгБДеИЗгБ£гБ¶еЕ•гБ£гБ¶гБњгБЊгБЧгВЗгБЖгАВ
гБЧгБЛгБЧгБ¶еЗЇгБ¶гБНгБЯгГЯгВљгГ©гГЉгГ°гГ≥гАБгБЊгБХгБЂжЬ™зЯ•гБ®гБЃйБ≠йБЗпЉИжВ™гБДжДПеС≥гБІпЉЙгАВ
жГ≥еГПгБЃгБѓгВЛгБЛжЦЬгВБдЄКгАБи®ШжЖґгБЂжЃЛгВЛгБЊгБЪгБХгБІгБЧгБЯгАБгБ®гАВ
гБХгБ¶гАБгБЭгВМгБІгБѓжђ°гБЃеЗЇеЉµжЩВгАБгБВгБ™гБЯгБѓгБУгБЃгГ©гГЉгГ°гГ≥е±ЛгБЂеЕ•гВКгБЊгБЩгБЛпЉЯ
гАМдЇМеЇ¶гБ®гБФгВБгВУгБ†гАНгБ®гБ™гВЛгБЛгВВзЯ•гВМгБЊгБЫгВУгАВ
гБІгВВиАГгБИгБ¶гБњгВЛгБ®гАБжХ∞гБВгВЛгГ°гГЛгГ•гГЉгБЃдЄ≠гБІгБВгБ™гБЯгБМй£ЯгБєгБЯгБЃгБѓгГЯгВљгГ©гГЉгГ°гГ≥гБЃдЄАеУБгБ†гБСгАВ
гБ≤гВЗгБ£гБ®гБЧгБЯгВЙгАБгБ®гВУгБУгБ§гГ©гГЉгГ°гГ≥гБѓзµґеУБгБЛгВВзЯ•гВМгБЊгБЫгВУгВИгАВ
гБВгБЃжЩВгБЊгБЪгБЛгБ£гБЯгБЃгБѓгБЯгБЊгБЯгБЊгБЛгАБеЇЧдЄїгБЃиЕХгБЃгБЫгБДгБ™гБЃгБЛгАВ
гБУгВМгБѓеИЗеЃЯгБ™еХПй°МгБІгБЩгБ≠гАВ
зЫЃжђ°
гБ©гБУгБЊгБІжЕОйЗНпЉЯ зІСе≠¶иАЕ3дЇЇзµДгБЃжО®иЂЦгГРгГИгГЂ
жђ°гБЂз§ЇгБЩгБЃгБѓгАБзІСе≠¶зЪДжО®иЂЦгБЂйЦҐгБЩгВЛжЬЙеРНгБ™йАЄи©±гАВ

зФїеГПпЉЪзІСе≠¶иАЕгБЯгБ°гБЃжО®иЂЦ иСЧиАЕдљЬжИР
гБУгВМгБѓгАМеО≥еѓЖгБ™жАЭиАГгАНгБЃдЊЛгБИгБ®гБЧгБ¶иЂЦзРЖе≠¶гВДзІСе≠¶еУ≤е≠¶гБЃжЦЗиДИгБІгВИгБПдљњгВПгВМгВЛгАБ詆гБњдЇЇгБЧгВЙгБЪгБЃжЬЙеРНгБ™йАЄи©±гБІгБЩгАВ
гБЊгБЪгБѓе§©жЦЗе≠¶иАЕгБХгВУгАБгБВгБЯгБЛгВВгВєгВ≥гГГгГИгГ©гГ≥гГЙгБЃзЊКгБЩгБєгБ¶гБМйїТгБДгБЛгБЃгВИгБЖгБЂзЩЇи®АгБЧгБ¶гБДгБЊгБЩгАВ
гБУгВМгБѓеЃЯйЪЫгБЃи¶≥жЄђгБЃйЩРеЃЪжАІгБЛгВЙгБЩгВЛгБ®гАБгБЭгБУгБЛгВЙе∞ОгБНеЗЇгБЩзµРиЂЦгБ®гБЧгБ¶гБѓдЄАиИђеМЦгБЧгБЩгБОгБІгБЩгБ≠гАВ
гБЭгВМгБЂжѓФгБєгВМгБ∞2зХ™зЫЃгБЃзЙ©зРЖе≠¶иАЕгБХгВУгАБгБЯгБ†1гБ§гБЃи¶≥жЄђдЇЛдЊЛгВТгВВгБ£гБ¶гБЧгБ¶дЄЛгБЩзµРиЂЦгБ®гБЧгБ¶гБѓгВИгВК嶕ељУгБ™гВВгБЃгБ®и®АгБИгБЊгБЩгАВ
зµРиЂЦгБЃдЄАиИђеМЦгБЂеѓЊгБЧжЕОйЗНгБІгБВгВКгАБзЙєеЃЪгБЃзПЊи±°гБЃе≠ШеЬ®гБЃгБњгВТдЄїеЉµгБЧгБ¶гБДгБЊгБЩгАВ
жЬАеЊМгБЃжХ∞е≠¶иАЕгБХгВУгБѓгАБгБЭгБЃжДПеС≥гБІгБѓжЕОйЗНгБХMAXгАВ
зЊКгБЃдљУгБЃзЙЗйЭҐгВТеИЧиїКгБЃз™УгБЛгВЙи¶ЛгБЯгБЂйБОгБОгБ™гБДгБ®гБДгБЖи¶≥жЄђдЇЛеЃЯгАБгБУгБЃжЭ°дїґгБЂеО≥еѓЖгБЂж≤њгБ£гБЯзµРиЂЦгБ•гБСгВТгБЧгБ¶гБДгБЊгБЩгАВ
зІСе≠¶зЪДжО®иЂЦгБЃдїХжЦєгБ®гБЧгБ¶гБѓгАБи¶≥жЄђгБЛгВЙеЊЧгВЙгВМгВЛжГЕ冱гБЃйЩРзХМгВТж≠£гБЧгБПи™Ни≠ШгБЧгБ¶гБДгВЛгБ®и®АгБИгБЊгБЩгАВ
гБЊгБВгБЧгБЛгБЧгАБеЃЯйЪЫеХПй°МгБ©гБЖгБІгБЩгБЛпЉЯ
жЧ•еЄЄзФЯжіїгБІгБУгБЃжХ∞е≠¶иАЕгБњгБЯгБДгБЃгБМзЫЃгБЃеЙНгБЂгБДгБЯгВЙгАБгБЭгБЃдЇЇгБ®ж•љгБЧгБПдЉЪи©±гБ®гБДгБЖгБЃгБѓгБ°гВЗгБ£гБ®зД°зРЖгБЛгВВгБЧгВМгБЊгБЫгВУгБ≠гАВ
гБЭгБЧгБ¶ељУзДґгБ™гБМгВЙгАБгБУгБЃйАЄи©±гБѓзЙ©зРЖе≠¶иАЕгВД姩жЦЗе≠¶иАЕгБЂеѓЊгБЩгВЛжХ∞е≠¶иАЕгБЃеД™иґКжАІгВТдЄїзЬЉгБ®гБЩгВЛгВВгБЃгБІгБѓгБВгВКгБЊгБЫгВУгАВ
зІБгБЯгБ°гБМгБУгБЃйАЄи©±гБЛгВЙж±≤гВАгБєгБНжХЩи®УгБѓгАБдЇЇгБѓеЊЧгБ¶гБЧгБ¶ж†єжЛ†гБ™гБПгАБгВВгБЧгБПгБѓеНБеИЖгБ™ж†єжЛ†гВТжМБгБЯгБЪгБЂзЙ©дЇЛгВТж±ЇгВБгБ§гБСгВЛеВЊеРСгБМгБВгВКгБЊгБЩгВИгАБгБ®гБДгБЖгБУгБ®гАВ
и¶≥еѓЯгГЗгГЉгВњгБЃеПЦеЊЧгБМеЊАгАЕгБЂгБЧгБ¶еЫ∞йЫ£гБ™е§©жЦЗе≠¶гБѓгАБ祯гБЛгБЂе∞СгБ™гБДгВµгГ≥гГЧгГЂгБЛгВЙдЄАиИђзЪДгБ™зµРиЂЦгВТеЗЇгБЩгБУгБ®гБМжѓФиЉГзЪДе§ЪгБДеИЖйЗОгБІгБѓгБВгВКгБЊгБЩгАВ
гБІгВВгБ†гБЛгВЙгБ®и®АгБ£гБ¶гАМ姩жЦЗе≠¶иАЕгБѓвА•гАНгБ®зµРиЂЦдїШгБСгВЛгБ®гБЩгВМгБ∞гАБгБЭгБЃиЂЦж≥ХиЗ™дљУгБМдЄАиИђеМЦгБЧгБЩгБОгБ®и®АгБИгВЛгБІгБЧгВЗгБЖгАВ
жХ∞е≠ЧгБЃдЄ¶гБ≥гБЃгГЂгГЉгГЂгВТ祯гБЛгВБгВИгБЖ
дї•дЄЛгБѓгГ≠гГ≥гГЙгГ≥е§Іе≠¶гБІи°МгВПгВМгБЯгАБгБ®гБВгВЛи™НзЯ•ењГзРЖе≠¶гБЃеЃЯй®УгБІгБЩгАВ

зФїеГПпЉЪењГзРЖе≠¶еЃЯй®УгБЃгБКй°МпЉСгААиСЧиАЕдљЬжИР

зФїеГПпЉЪењГзРЖе≠¶еЃЯй®УгБЃгБКй°МпЉТгААиСЧиАЕдљЬжИР
гВВгБ°гВНгВУгАМпЉТпЉМпЉФпЉМпЉЦгАНгБѓгБУгБЃгГЂгГЉгГЂгБЂеЊУгБ£гБ¶гБДгБЊгБЩгАВ
гБХгБ¶гАБгБЭгБЃгГЂгГЉгГЂгБ®гБѓгБ©гБЃгВИгБЖгБ™гВВгБЃгБІгБЧгВЗгБЖгАВ
гБВгБ™гБЯгБѓгБ©гВУгБ™жХ∞е≠ЧгБЃзЊЕеИЧгВТдљЬгБ£гБ¶и≥™еХПгБЧгБЊгБЩгБЛпЉЯ
еЃЯйЪЫгБЂгВИгБПжМЩгБТгВЙгВМгБЯи≥™еХПгБЃдЇЛдЊЛгБМгАБ
вЧЛеБґжХ∞гБЃеИЧпЉИгАМ8пЉМ10пЉМ12гАНгБ™гБ©пЉЙгАБ
гВВгБЧгБПгБѓ
вЧЛз≠ЙйЦУйЪФгБЃжХ∞еИЧпЉИгАМ10, 20, 30гАНгБ™гБ©пЉЙгАВ
祯гБЛгБЂгБ©гБ°гВЙгВВгАБгАМ2, 4, 6гАНгБЛгВЙеЃєжШУгБЂй°ЮжО®гБХгВМгВЛгВВгБЃгБІгБѓгБВгВКгБЊгБЩгАВ
гБІгБѓгАБеЃЯйЪЫгБЃгГЂгГЉгГЂгБѓгБ©гБЖгБ†гБ£гБЯгБЃгБІгБЧгВЗгБЖгБЛпЉЯ
гБЭгВМгБѓгАБеНШгБЂгАМеҐЧе§ІгБЩгВЛжХ∞еИЧгАНгБ†гБ£гБЯгБЃгБІгБЩгАВ
гГЩгГ≥еЫ≥гБІи°®гБЩгБ®гАБеЫ≥гБЃгВИгБЖгБЂгБ™гВКгБЊгБЩгАВ
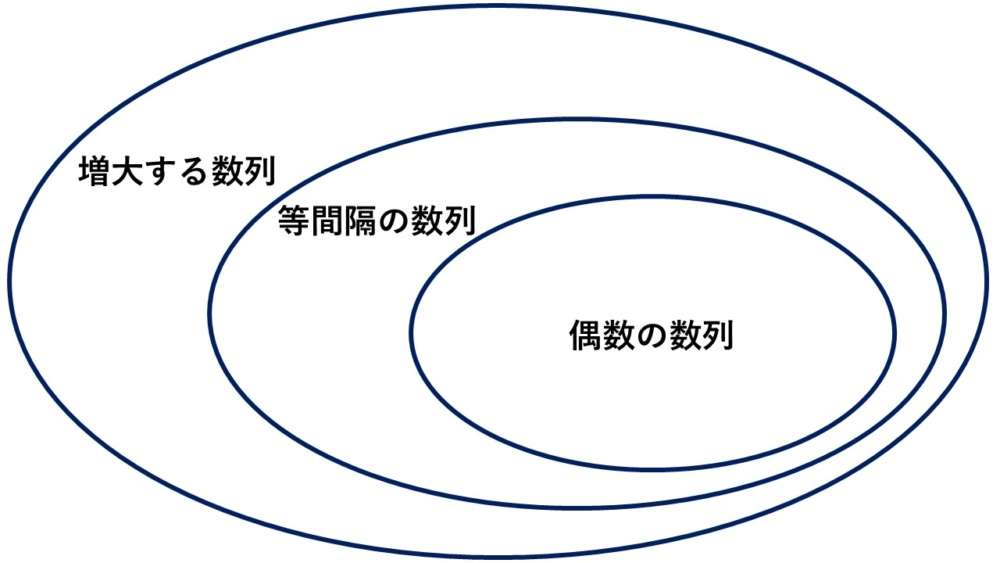
зФїеГПпЉЪгГЩгГ≥еЫ≥гААиСЧиАЕдљЬжИР
ељУзДґгБ™гБМгВЙгАБгАМеҐЧе§ІгБЩгВЛжХ∞еИЧгАНгБѓгБУгБЃдЄ≠гБІгБѓдЄАзХ™еЇГгБДгАВ
гАМеБґжХ∞гБЃеИЧгАНгБМжЬАгВВзЛ≠гБДгВЂгГЖгВігГ™гГЉгБ®гБ™гВКгБЊгБЩгАВ
еЃЯйЪЫгБЃеЃЯй®УгБІиҐЂй®УиАЕгБЯгБ°гБЛгВЙеЗЇгБХгВМгБЯи≥™еХПгБѓгАБгБУгБЃгАМеБґжХ∞гБЃдЄ¶гБ≥гАНгВДгАМз≠ЙйЦУйЪФгБЃжХ∞е≠ЧгБЃдЄ¶гБ≥гАНгВТжГ≥еЃЪгБЧгАБгБЭгБЃж≠£гБЧгБХгВТ祯гБЛгВБгВЛз≠ФгБИпЉИгАМ8, 10, 12гАНгВДгАМ10, 20, 30гАНгБЃгВИгБЖгБ™пЉЙгБ∞гБЛгВКгБІгБЧгБЯгАВ
ељЉгВЙгБМеЊЧгВЛеЫЮз≠ФгБѓеЄЄгБЂYESгАВ
гБ†гБ£гБ¶гБ©гВМгВВеҐЧе§ІгБЩгВЛжХ∞е≠ЧгБІгБЩгБЛгВЙгАВ
гБЧгБЛгБЧгАБељЉгВЙгБМжГ≥еЃЪгБЧгБЯгГЂгГЉгГЂгБѓйЦУйБХгБ£гБ¶гБДгВЛгАВ
гБУгБЃгБУгБ®гБѓдљХгВТжДПеС≥гБЩгВЛгБЃгБІгБЧгВЗгБЖгБЛгАВ
и™НзЯ•гБЃеБПгВКгАМ祯變гГРгВ§гВҐгВєгАН
иЗ™еИЖгБЃжГ≥еЃЪгБЃж≠£гБЧгБХгВТ祯гБЛгВБгВИгБЖгБ®гБЩгВЛгБУгБЃеВЊеРСгБѓгАМ祯變гГРгВ§гВҐгВєгАНгБ®еСЉгБ∞гВМгБЊгБЩгАВ
гГРгВ§гВҐгВєгБ®гБѓгАМеБПгВКгАНгАВ
дЇЇгБЃи™НзЯ•ж©ЯиГљгБЂгБѓгАБгБУгБЃеБПгВКгБМеЖЕеЬ®гБХгВМгБ¶гБДгБЊгБЩгАВ
祯變гГРгВ§гВҐгВєгБМгБВгВЛгБЯгВБгБЂгАБдЇЇгБѓиЗ™еИЖгБЃиАГгБИгБМж≠£гБЧгБПгБ™гБДгБУгБ®гВТгБ™гБЛгБ™гБЛжГ≥еЃЪгБЩгВЛгБУгБ®гБМгБІгБНгБЊгБЫгВУгАВ
йЦУйБХгБ£гБ¶гБДгВЛеПѓиГљжАІгВТиАГгБИгБ¶и°МеЛХгБЩгВЛгБУгБ®гБМгБІгБНгБ™гБДгБЃгБІгБЩгАВ
гВВгБЧгАМгБУгВМгБѓеБґжХ∞гБЃеИЧгБ†гВНгБЖгАНгБ®жАЭгБ£гБЯгБ®гБЧгБ¶гВВгАБгБЭгБЖгБШгВГгБ™гБДеПѓиГљжАІгАБдЊЛгБИгБ∞еБґжХ∞гБ®е•ЗжХ∞гБЃжЈЈгБЦгБ£гБЯжХ∞еИЧгАБгАМ8, 9, 12гАНгВТжПРз§ЇгБЧгВИгБЖгБ®жАЭгБИгБ∞гБІгБНгБЊгБЩгАВ
гВВгБЧзЦСгБДгВТжМБгБ°гАБгГПгВЇгГђгБ†гВНгБЖгБ®гБѓжАЭгБДгБ§гБ§гВВгАМ8, 9, 12гАНгВТжПРз§ЇгБЧгБЯгВЙгБ©гБЖгБ™гВЛгБЛпЉЯ
гБЭгБЃз≠ФгБИгБѓпЉИиЗ™еИЖгБЃдЇИжГ≥гБЂеПНгБЧгБ¶пЉЙ”Yes”гАВ
гБУгБУгБІеИЭгВБгБ¶гАБж±ВгВБгБЯгБДгГЂгГЉгГЂгБМгАМеБґжХ∞гБЃеИЧгАНгБІгБѓгБ™гБДгБУгБ®гБЂж∞ЧгБ•гБПгБЃгБІгБЩгАВ
гБ†гБМгАБгБЭгБЖгБѓгБЧгБ™гБДгАВ
гБїгБ®гВУгБ©гБЃдЇЇгБМеБґжХ∞гБЃеИЧгБШгВГгБ™гБДи≥™еХПгВТгБЩгВЛгБ®гБДгБЖзЩЇжГ≥гБЂиЗ≥гВЙгБЪгАБ虧гБ£гБЯгГЂгГЉгГЂгВТж≠£иІ£гБ®жАЭгБДиЊЉгБњгБЭгБЃзҐЇи™НгВТгБЩгВЛгБ†гБСгБІгБЧгБЯгАБ祯變гГРгВ§гВҐгВєгБЃгБЯгВБгБЂгАВ
дЇЇгБѓзЯ•гВЙгБ™гБДгБЖгБ°гБЂгАМгВЄгГ£гГ≥гГЧгАНгБЩгВЛгБЃгБІгБЩгАВ
гГФгГ≥гВѓгБЃеГПгБЛгВЙиЗ™зФ±гБЂгБ™гВНгБЖ
дЇЇгБѓжАЭгБДгБЃгБїгБЛгАБж†єжЛ†гБ™гБПзЙ©дЇЛгВТж±ЇгВБгБ§гБСгВЛеВЊеРСгБМгБВгВЛгБ®гБДгБЖгБУгБ®гБІгБЩгБ≠гАВ
гБЭгВМгБѓгАБзІСе≠¶иАЕгВВгВВгБ°гВНгВУдЊЛе§ЦгБІгБѓгБВгВКгБЊгБЫгВУгАВ
иЂЦзРЖзЪДгБЂиАГгБИгВМгБ∞зµРиЂЦгВТеЗЇгБЫгБ™гБДгБУгБ®гВДзЦСеХПгБМжЃЛгВЛгБѓгБЪгБЃгБУгБ®гВТдЄАж∞ЧгБЂй£ЫгБ≥иґКгБИгАБгБВгВЛзµРиЂЦгВТеЗЇгБЩгАБгБ®гАВ
зІСе≠¶з†Фз©ґгБЂгБКгБДгБ¶гВВгАБгБЭгБЃгВИгБЖгБ™иЂЦзРЖгБЃгВЄгГ£гГ≥гГЧгБѓи®±гБХгВМгБЊгБЫгВУгАВ

зФїеГПпЉЪгВЄгГ£гГ≥гГЧгБЩгВМгБ∞гВИгБДгБ®гБДгБЖгВВгБЃгБІгБѓвА•гААиСЧиАЕдљЬжИР
дЄАж≠©дЄАж≠©жЃµйЪОгВТиЄПгБњгАБгБЖгБЃгБњгБЂгБЫгБЪзЦСеХПгВТжМБгБ°гАБзЪЖгБІзҐЇгБЛгВБеРИгБДгБ™гБМгВЙгАБе∞СгБЧгБЪгБ§йА≤гВУгБІгБДгБПгБЃгБІгБЩгАВ
祯變гБЃеЊЧгВЙгВМгБЯдЇЛеЃЯдї•е§ЦгБѓгАБеПѓиГљжАІгВТжМЗжСШгБЩгВЛгБЂгБ®гБ©гВБгВЛгАВ
зІСе≠¶иАЕгБЃи≠∞иЂЦгБѓгАБгВИгБПж≠ѓеИЗгВМгБМжВ™гБДгБ®и®АгВПгВМгБЊгБЩгАВ
гАМдїКеЊМ30еєідї•еЖЕгБЂгГЮгВ∞гГЛгГБгГ•гГЉгГЙпЉШз®ЛеЇ¶гБЃеЬ∞йЬЗгБМиµЈгБУгВЛ祯зОЗгБѓвЧЛвЧЛпЉЕгАНгБ™гБ©гБІгБЩгАВ
гБЭгВМгБѓгВДгВАгВТеЊЧгБ™гБДгБУгБ®гБІгБВгВКгАБжЬђи≥™зЪДгБЂзІСе≠¶иАЕгБѓжЕОйЗНгГїиђЩиЩЪгБ™гВВгБЃгАВ
гБЊгБЯгАБгБЭгБЖгБДгБ£гБЯжЕЛеЇ¶гБУгБЭгБМгАБгАМзІСе≠¶зЪДгАНгБІгБВгВЛгБУгБ®гБЃй™®й†ВгБІгВВгБВгВЛгБЃгБІгБЩгАВ
жЦЗ / з®ЃеЄВ е≠ЭпЉИгБЯгБ≠гБДгБ°гБЯгБЛгБЧпЉЙж†°ж≠£ / иНЙгБЃеЃЯе†ВзЈ®йЫЖйГ®






















гБУгБЃи®ШдЇЛгБЄгБЃгВ≥гГ°гГ≥гГИгБѓгБВгВКгБЊгБЫгВУгАВ