筆者は超心理物理学者として、よく一般向けに科学関連のトピックや最先端の研究分野について講演をすることがあります。
するとたまに、「究極の物理理論は存在すると思うか?」などという質問をされることがあります。
「究極」、そのココロはこの宇宙の姿をあまねく記述し、そこで生起する全ての現象を予測し説明できる、という意味。
そんな理論、果たして存在するのでしょうか。
「私は正しい」はダメ

画像:宇宙の深淵に想いを馳せる 著者作成
筆者は、以下の二つの理由で「それは存在しない」とお答えしています。
理由の一つ目は、人類の知覚や思考力、技術力、知識、そのどれをとっても限界があり、また技術は発展すると言っても有限時間には有限の発展しかしないのであり、人類の認知が到達し得ない自然界の深淵が存在するであろうことは間違いないこと。
この言明は、科学的なアプローチでこの宇宙・自然を理解しようと不断の努力を続けることの重要さ、に軸足を置いています。
「ここから先は人類の認知が到達し得ない領域」を勝手に設定し、最後は神などの超自然的存在に身をゆだねる立場の表明ではありません。
二つ目は、ある理論が正しいことを、その理論自身を用いて証明することが不可能であること。
これはゲーデルの不完全性定理として知られます。
ある理論が正しいことを、その理論の範囲内で証明することはできません。
必ずその理論の外側にある他の理論に基づかなければ、正しさを証明することはできないのです。
究極の理論などというものを想定すること、それは自己矛盾をはらんでいるのに気づきますか?
その理論は、究極であるがゆえに自分自身が正しい理由も説明することになる。
これはナンセンスです。
ちなみに実験的に証明しようとするなら、たちまち先に挙げた一つ目の事由に抵触します。
19世紀に訪れた高揚
歴史的には、「究極の理論に到達した」感が物理学者を席巻したことが実はあります。
それは19世紀の終わりごろ。
今では古典物理学の部類に入るニュートン力学とマクスウェルの電磁気学。
これで幸か不幸かこの世の森羅万象すべてが説明できる、と思われたのでした。
全てを知り尽くしてラッキー?
基礎部門の物理学者、総失職でアンラッキー?
技術に知識が追い付かない

画像:溶鉱炉 著者作成
しかして、その究極の理論とやらのほころびは産業革命から。
18世紀後半から19世紀にかけて、大きな質的・量的変化を遂げた産業界。
その中でも中核的だった製鉄業において、溶鉱炉の中の温度測定は重要な技術でした。
もちろん溶けた鉄に温度計を指して測定、という訳にはいきません。
溶鉱炉から発せられる光のその波長分布、つまり発光スペクトルによって温度を見積もる必要があります。
最近はほとんど見かけなくなりましたが、電気コンロやストーブなどに使用される電熱線に通電すると、温度上昇と共に赤みを帯び始め、やがて赤く輝くようになります。
さらに温度が上がると色は赤から黄色、そして白っぽい色へと変化し、明るさも増していきます。
色の違いは波長の違い。
それを利用して、溶鉱炉からの光のスペクトルを測定することにより、その波長成分から温度を割り出そう、という訳です。
割り出すためには温度と波長の対応を理論的にもとめ、実際の観測データをそれと対照させなくてはなりません。
観測と整合しない理論
スペクトル測定そのものは、当時わりと精密にできました。
しかしそれと比較すべき理論式、これが完成しなかった。
いや、理論式自体はあったのです、2つも。
今日では「レイリー・ジーンズの式」、そして「ウィーンの式」として知られます。
どちらも当時の「究極理論」式に求められたものです。
しかしこれがうまく行かない。
どちらも観測事実と一致しない。
それどころか、これら2つの式どうしがまた相矛盾しているという、ほとんど病的な状況に。
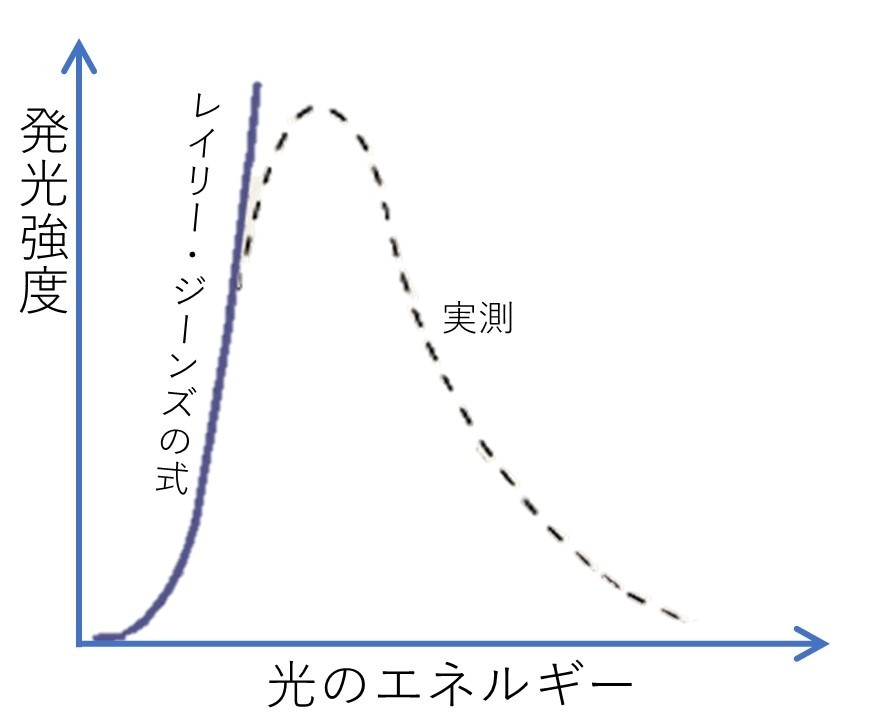
レイリー・ジーンズの式は光のエネルギー密度、つまり一定体積当たりのエネルギーが光の振動数によって異なる、という事実をベースに組み立てられました。
この式は低エネルギー領域、つまり波長の長い領域で光の波長が短いほど光の強度が大きいことを示し、実験結果の波形と見事に一致。
しかし、高エネルギー領域(短波長側)では発散、つまり無限大となってしまうという不都合がありました。
画像:レイリー・ジーンズの式 著者作成
古典物理学(当時の「究極」理論)では、物体のエネルギーは連続的に変化できるとされます。
有限の振動数域でも、そこに対応する振動数を持った光の種類の数(モード数)は膨大になるため、全体では光のエネルギーが無限大に発散してしまうのです。
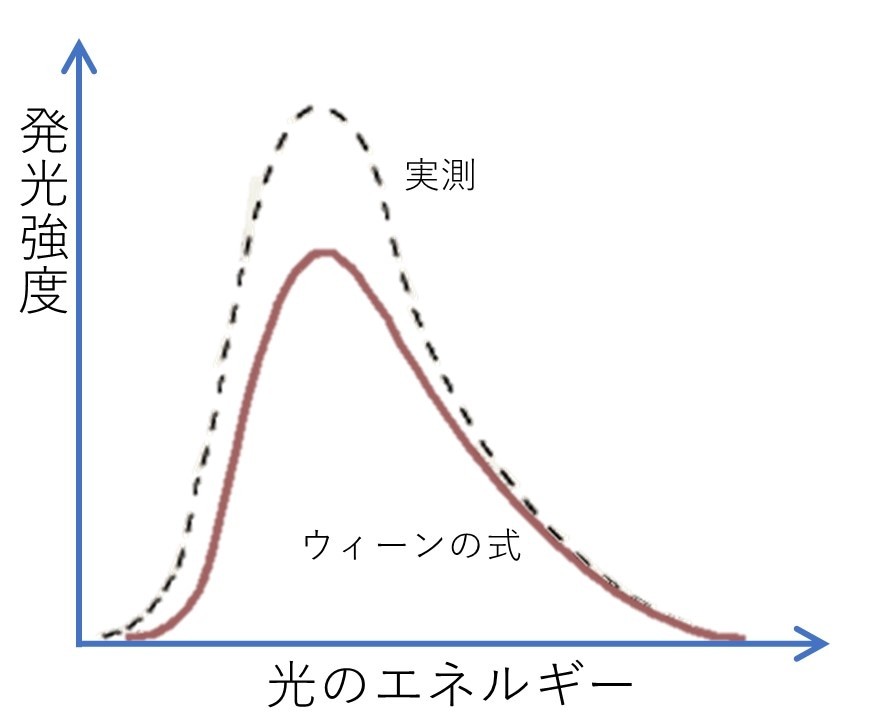
一方のウィーンの式はというと、これはスペクトルのピーク(山の頂上部分)における振動数(波長の逆数)と、その時の光を発する物体の温度との比が一定になるという経験則から導かれたもの。
これは逆に高エネルギー側で実験結果と一致するのですが、低エネルギー側では一致せず。
画像:ウィーンの式 著者作成
さらにこの式は、理論モデルから導出されたものではなく経験則。
高エネルギー側で一致すると言っても、じゃあなぜそれが一致するのか、を説明することはできません。
救いの手は「量子仮説」
この古典物理学のほころびにメスを入れ、物理学を古典から現代版に昇華させるきっかけとなったのが「プランクの量子仮説」です。
エネルギーは連続的に変化できるのは常識と思われていましたが、それを敢えて不連続であると限定し、離散的、つまり飛び飛びの値しか取れないと仮定したのでした。
これで高エネルギー側、低エネルギー側双方で、測定されるスペクトルの形を再現する理論式を人類は手にすることができました。
しかし、それでもプランク本人は最初のうち、エネルギー値が飛び飛びとなることをなかなか信じることができなかったそうです。
と言うか、彼自身はそんなことを前提とすらしておらず、測定結果に合う式をまずは考えようとしていたのでした。
しかし結果としてこの式が、というよりエネルギー値が離散的というこの概念こそが、その後の量子力学構築の礎となりました。
現状の物理学はどうか
今日、私たちが手にしている現代物理学の二大主要理論、それは量子論と相対論です。
これらはよく調べてみると、実は根本のところで相矛盾するという弱点を有しています。
その詳細は置いておくとして、これらが矛盾しているという事実は、19世紀のニュートン力学とマクスウェルの電磁気学のような関係とも異なり、私たちが究極の理論など手に入れていないということを明瞭に示していると言えます(※)。
(※)細かいことを言うと、座標変換に対する不変性という観点で見れば、実はニュートン力学と電磁気学とはすでに矛盾しており、その意味で究極とは言えないことを当時の物理学者も気づいていました。
これらを統一した新たな理論が将来見つかったとして、ではそれは究極と言えるのか?
そうとは言えないでしょう。
理由は冒頭に示した通り。
けれども、その新理論がほころびを見せるような極限的な現象を人類が目にするより先に、人類が滅亡してしまうなんてことがあるかも知れません。
だとするなら人類史的にはその新理論が「究極の理論」、と言えるのかもしれません、やや悲観的ではありますが。
文 / 種市孝(たねいちたかし)























この記事へのコメントはありません。