出張先で腹が減った時、ふと前を見るとそこにラーメン屋。

チェーン店ではなく、見たこともない店名です。

こういうのって、入るのにちょっと勇気いりますよね？

でも今はとても腹が減っている。

ほかに店も見当たらないし、背に腹はかえられん。

思い切って入ってみましょう。

しかして出てきたミソラーメン、まさに未知との遭遇（悪い意味で）。

想像のはるか斜め上、記憶に残るまずさでした、と。

さて、それでは次の出張時、あなたはこのラーメン屋に入りますか？

「二度とごめんだ」となるかも知れません。

でも考えてみると、数あるメニューの中であなたが食べたのはミソラーメンの一品だけ。

ひょっとしたら、とんこつラーメンは絶品かも知れませんよ。

あの時まずかったのはたまたまか、店主の腕のせいなのか。

これは切実な問題ですね。

どこまで慎重？ 科学者3人組の推論バトル

次に示すのは、科学的推論に関する有名な逸話。

画像：科学者たちの推論 著者作成

これは「厳密な思考」の例えとして論理学や科学哲学の文脈でよく使われる、詠み人しらずの有名な逸話です。

まずは天文学者さん、あたかもスコットランドの羊すべてが黒いかのように発言しています。

これは実際の観測の限定性からすると、そこから導き出す結論としては一般化しすぎですね。

それに比べれば2番目の物理学者さん、ただ1つの観測事例をもってして下す結論としてはより妥当なものと言えます。

結論の一般化に対し慎重であり、特定の現象の存在のみを主張しています。

最後の数学者さんは、その意味では慎重さMAX。

羊の体の片面を列車の窓から見たに過ぎないという観測事実、この条件に厳密に沿った結論づけをしています。

科学的推論の仕方としては、観測から得られる情報の限界を正しく認識していると言えます。

まあしかし、実際問題どうですか？

日常生活でこの数学者みたいのが目の前にいたら、その人と楽しく会話というのはちょっと無理かもしれませんね。

そして当然ながら、この逸話は物理学者や天文学者に対する数学者の優越性を主眼とするものではありません。

私たちがこの逸話から汲むべき教訓は、人は得てして根拠なく、もしくは十分な根拠を持たずに物事を決めつける傾向がありますよ、ということ。

観察データの取得が往々にして困難な天文学は、確かに少ないサンプルから一般的な結論を出すことが比較的多い分野ではあります。

でもだからと言って「天文学者は‥」と結論付けるとすれば、その論法自体が一般化しすぎと言えるでしょう。

数字の並びのルールを確かめよう

以下はロンドン大学で行われた、とある認知心理学の実験です。

画像：心理学実験のお題１　著者作成

画像：心理学実験のお題２　著者作成

もちろん「２，４，６」はこのルールに従っています。

さて、そのルールとはどのようなものでしょう。

あなたはどんな数字の羅列を作って質問しますか？

実際によく挙げられた質問の事例が、

○偶数の列（「8，10，12」など）、

もしくは

○等間隔の数列（「10, 20, 30」など）。

確かにどちらも、「2, 4, 6」から容易に類推されるものではあります。

では、実際のルールはどうだったのでしょうか？

それは、単に「増大する数列」だったのです。

ベン図で表すと、図のようになります。

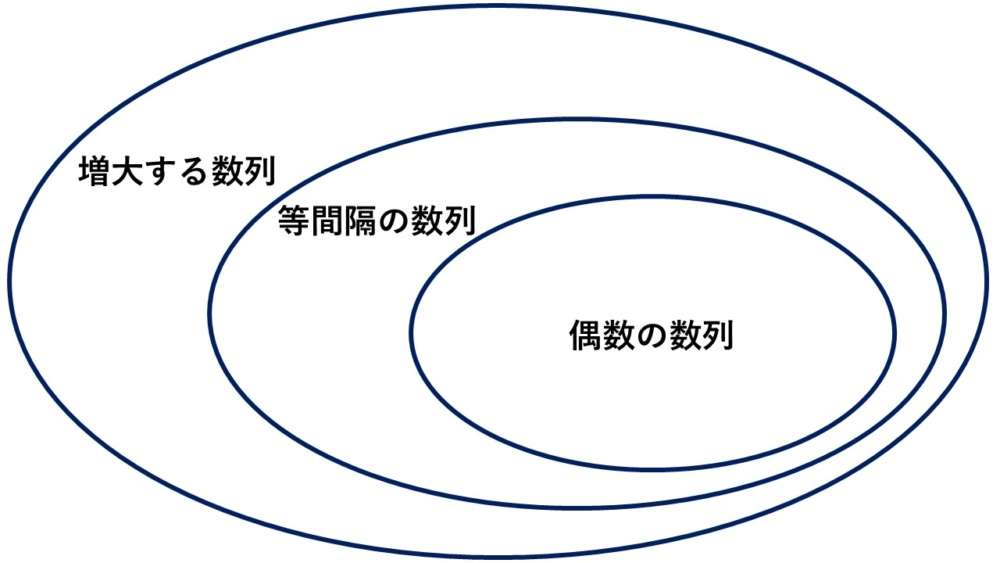
画像：ベン図　著者作成

当然ながら、「増大する数列」はこの中では一番広い。

「偶数の列」が最も狭いカテゴリーとなります。

実際の実験で被験者たちから出された質問は、この「偶数の並び」や「等間隔の数字の並び」を想定し、その正しさを確かめる答え（「8, 10, 12」や「10, 20, 30」のような）ばかりでした。

彼らが得る回答は常にYES。

だってどれも増大する数字ですから。

しかし、彼らが想定したルールは間違っている。

このことは何を意味するのでしょうか。

認知の偏り「確証バイアス」

自分の想定の正しさを確かめようとするこの傾向は「確証バイアス」と呼ばれます。

バイアスとは「偏り」。

人の認知機能には、この偏りが内在されています。

確証バイアスがあるために、人は自分の考えが正しくないことをなかなか想定することができません。

間違っている可能性を考えて行動することができないのです。

もし「これは偶数の列だろう」と思ったとしても、そうじゃない可能性、例えば偶数と奇数の混ざった数列、「8, 9, 12」を提示しようと思えばできます。

もし疑いを持ち、ハズレだろうとは思いつつも「8, 9, 12」を提示したらどうなるか？

その答えは（自分の予想に反して）”Yes”。

ここで初めて、求めたいルールが「偶数の列」ではないことに気づくのです。

だが、そうはしない。

ほとんどの人が偶数の列じゃない質問をするという発想に至らず、誤ったルールを正解と思い込みその確認をするだけでした、確証バイアスのために。

人は知らないうちに「ジャンプ」するのです。

ピンクの像から自由になろう

人は思いのほか、根拠なく物事を決めつける傾向があるということですね。

それは、科学者ももちろん例外ではありません。

論理的に考えれば結論を出せないことや疑問が残るはずのことを一気に飛び越え、ある結論を出す、と。

科学研究においても、そのような論理のジャンプは許されません。

画像：ジャンプすればよいというものでは‥　著者作成

一歩一歩段階を踏み、うのみにせず疑問を持ち、皆で確かめ合いながら、少しずつ進んでいくのです。

確証の得られた事実以外は、可能性を指摘するにとどめる。

科学者の議論は、よく歯切れが悪いと言われます。

「今後30年以内にマグニチュード８程度の地震が起こる確率は○○％」などです。

それはやむを得ないことであり、本質的に科学者は慎重・謙虚なもの。

また、そういった態度こそが、「科学的」であることの骨頂でもあるのです。

文 / 種市 孝（たねいちたかし）校正 / 草の実堂編集部